24.12.2020
Уроки 41, 42
Урок 41
Тема. Дослідження руху тіла, кинутого під кутом до горизонту.
Завдання:
- Переглянути відео (нище, за посиланням)
- Записати конспект з відео в зошит
- Записати розв'язок задач в зошит
РУХ ТІЛА, КИНУТОГО ПІД КУТОМ ДО ГОРИЗОНТУ
Задача № 1
Тіло кидають під кутом 300 до горизонту з початковою швидкістю 40 м/с. Знайдіть час польоту тіла. Визначте дальність польоту тіла та його максимальну висоту підняття. Знайдіть час підйому та опускання тіла.
Розв’язання:
І. ЗНАЙДЕМО ДАЛЬНІСТЬ ПОЛЬОТУ ТІЛА. ЧАС ПОЛЬОТУ ТІЛА: На схемі руху позначимо початкову та кінцеву координати, вектори початкової, кінцевої швидкості та прискорення тіла (рис 1).
4) Спроектуємо зазначені вектори на вісь (рис 2). | 1) Побудуємо схему руху, пов’язавши систему відліку з землею. На рисунку 1 та 2 зображена траєкторії руху тіл. 2) Оскільки рух відбувається у площині, то для його описання потрібно взяти дві взаємо перпендикулярні осі координат OX та OY. 3) Для полегшення розв’язку задачі вважатимемо, що вісь координат ОY напрямлена вертикально вгору, а вісь OX – горизонтальна і направлена вздовж руху тіла, та в момент час t0=0 тіло знаходились в точці перетину осей, тобто в початку координат.  |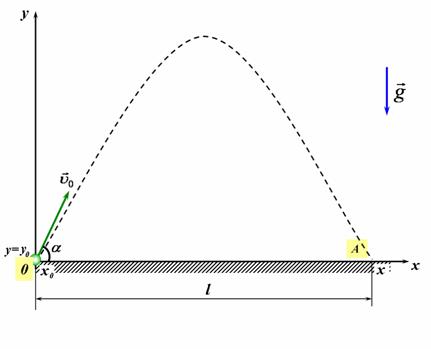
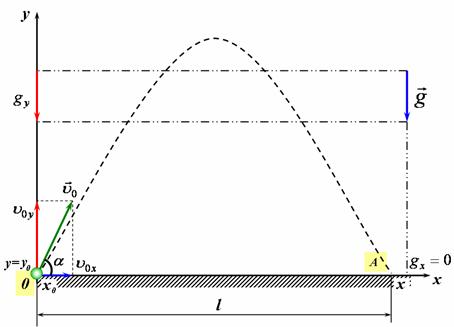
40 м/с
-?
-?
5) Для знаходження дальності польоту тіла l запишемо рівняння руху для тіла в проекціях на осі координат від моменту, коли тіло почало рух, до моменту його падіння на землю:
Вісь ОХ
Визначимо, чому дорівнюють відповідні коефіцієнти в рівнянні для нашого конкретного випадку:
Підставимо відповідні значення в рівняння руху:
| Вісь OY
Визначимо, чому дорівнюють відповідні коефіцієнти в рівнянні для нашого конкретного випадку:
Підставимо відповідні значення в рівняння руху:
|
В рівнянні (2) скоротимо на час польоту t та знайдемо цей час:
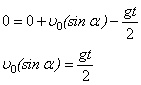
(*3) – час польоту тіла до падіння на землю.
Підставимо (3) в (1):
З математики відомо, що 
, тоді:
(*4) дальність польоту тіла
ЦІКАВО ПРОАНАЛІЗУВАТИ ОТРИМАНЕ СПІВВІДНОШЕННЯ:
З співвідношення (*4) слідує, що дальність польоту буде максимальною, при
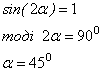
При 450 максимально можлива дальність польоту при фіксованому значенні 
буде дорівнювати:
ІІ. МАКСИМАЛЬНА ВИСОТА ПІДНЯТТЯ. ЧАС ПІДЙОМУ ТА СПУСКУ:
Час підйому – це час, протягом якої тіло рухатиметься від точки кидання до найвищої точки траєкторії.
Час спуску – це час, протягом якого тіло рухатиметься від найвищої точки траєкторії до поверхні землі.
Складемо схему руху для випадку руху тіла від моменту кидання до найвищої точки траєкторії (рис 3):
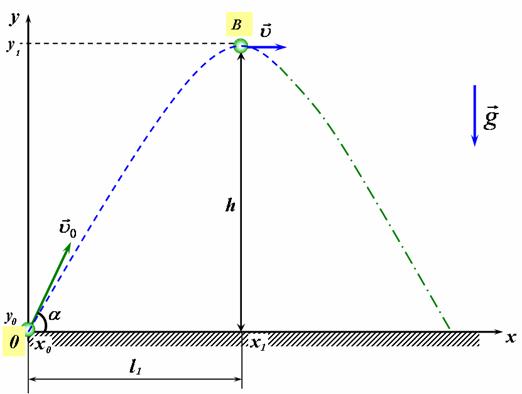
рис 3 |
Спроектуємо вектори швидкості та прискорення на осі координат (рис 4):
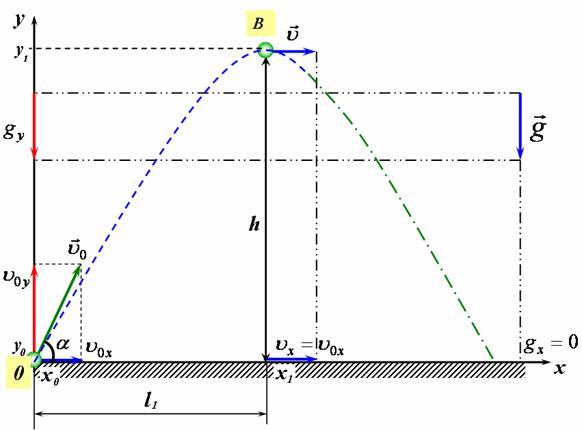
рис 4 |
Запишемо рівняння руху для переміщення тіла з точки А до найвищої точки траєкторії, точки В, в проекціях на вісь OY:
- час підйому;
Визначимо, чому дорівнюють відповідні коефіцієнти в рівнянні для нашого конкретного випадку:
Підставимо відповідні значення в рівняння руху:
(5)
Запишемо рівняння швидкості для переміщення тіла з точки А до найвищої точки траєкторії, точки В, в проекціях на вісь OY:
Визначимо, чому дорівнюють відповідні коефіцієнти в рівнянні для нашого випадку руху:
Підставимо відповідні значення в рівняння швидкості:
(6)
З рівняння (6) знайдемо час підйому :
(*7) – час підйому
Якщо час підйому порівняти з загальним часом руху (формула (*3)), то можна зробити висновок, що час підйому вдвічі менше за весь час руху, а отже час підйому дорівнюватиме часу спуску.
Підставимо (*7) в (*6):
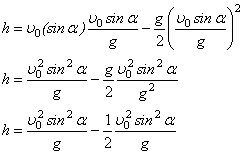
(*8) максимальна висота підняття тіла.
ЦІКАВО ПРОАНАЛІЗУВАТИ ОТРИМАНЕ СПІВВІДНОШЕННЯ:
ЦІКАВО ПРОАНАЛІЗУВАТИ ОТРИМАНЕ СПІВВІДНОШЕННЯ:
З співвідношення (*8) слідує, що дальність польоту буде максимальною, при
При 900 максимально можлива дальність польоту при фіксованому значенні буде дорівнювати:
Перевіримо розмірність:
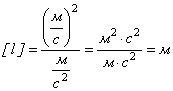
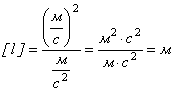
Виконаємо обчислення:
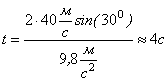
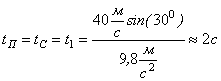
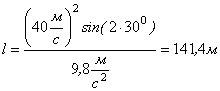
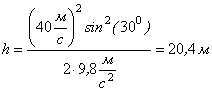
Відповідь: 
; 
; 
; 
Задача № 2
З гармати вистрілили снарядом. Швидкість снаряду =200 м/с, ствол гармати розташований під кутом 
=600 до горизонту. Знайдіть швидкість тіла через 5 с від моменту кидання.
Розв’язання:
| 1) Побудуємо схему руху, пов’язавши систему відліку з землею. На рисунку 1 та 2 зображена траєкторії руху тіл. 2) Оскільки рух відбувається у площині, то для його описання потрібно взяти дві взаємо перпендикулярні осі координат OX та OY. 3) Для полегшення розв’язку задачі вважатимемо, що вісь координат ОY напрямлена вертикально вгору, а вісь OX – горизонтальна і направлена вздовж руху тіла, та в момент час t0=0 тіло знаходились в точці перетину осей, тобто в початку координат. |
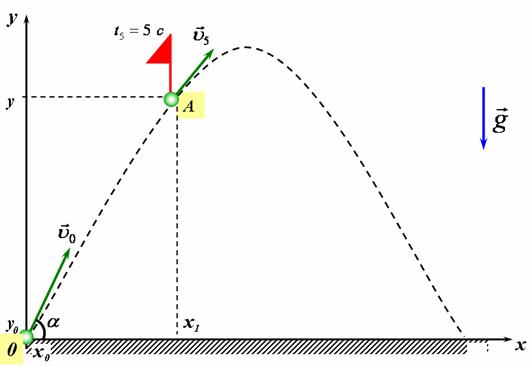
-? 3) Складемо схему руху для випадку руху тіла від моменту кидання до моменту падіння (рис 1) Вважатимемо, що в момент часу 
=5 c тіло буде знаходиться в точці А:
рис 1 |
Спроектуємо вектори швидкості та прискорення на осі координат (рис 2):
рис 2 |
Запишемо рівняння швидкості для переміщення тіла з точки О до точки А за час 
, в проекціях на вісь OY та на вісь ОХ:
Вісь ОХ
Визначимо, чому дорівнюють відповідні коефіцієнти в рівнянні для нашого конкретного випадку:
Підставимо відповідні значення в рівняння руху:
| Вісь OY
Визначимо, чому дорівнюють відповідні коефіцієнти в рівнянні для нашого конкретного випадку:
Підставимо відповідні значення в рівняння руху:
|
Тоді модуль швидкості 
можна знайти за теоремою Піфагора з утвореного трикутника 
:
 |
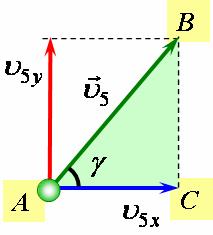Підставивши в останнє рівняння замість сторін трикутника значення довжин проекцій та модуль вектора, отримаємо:
(3)
Підставимо (2) та (1) в (3):
(*4)
Оскільки швидкість – це векторна величина, то крім величини характеризується ще й напрямком. Напрямок можна вказати з допомогою значення кута, який утворює даний вектор з осями координат 
.Знайдемо цей кут з :
(5)
Підставимо (1) та (2) в (5):
Виконаємо обчислення:
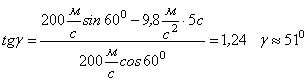
Відповідь: 
; 
Урок 42
Тема. Лабораторна робота. Дослідження руху тіла, кинутого під кутом до горизонту
Завдання:
- Виконати лабораторну роботу, дивлячись відео (нище за посиланням...лабораторна робота)
- Записати розрахунки в зошит (використовуючи відео)
- Скласти таблицю за прикладом
Лабораторна робота № 5
Тема: | Вивчення руху тіла, кинутого під кутом до горизонту, в полі сили тяжіння |
Мета: | дослідити рух тіла, кинутого під кутом до горизонту; визначити швидкість вильоту снаряду з моделі гармати; дослідити вид траєкторії руху тіла, кинутого під кутом до горизонту, у полі сили тяжіння. |
Обладнання: | установка для дослідження руху, кинутого під кутом до горизонту, тіла у полі сили тяжіння, вимірювальна стрічка, міліметровий папір, транспортир, пластилін, пластиковий стаканчик з водою, клейка стрічка (за необхідності). |
Теоретичні відомості
Механічний рух – це явище зміни положення тіла відносно інших тіл в просторі з часом. За характером траєкторії механічний рух поділяється на прямолінійний і криволінійний. Прямолінійним називають такий рух, при якому траєкторією руху тіла є пряма.
За характером зміни швидкості механічний рух поділяють на рівномірний і нерівномірний. Рівномірний рух – це рух при якому тіло за будь-які рівні проміжки часу проходить однакові шляхи. Тобто при рівномірному русі швидкість тіла не змінюється. Однак, рівномірного руху в природі не існує і тому особливий інтерес викликає вивчення нерівномірного руху, тобто такого руху, під час якого швидкість рухомого тіла змінюється.
Одним з видів нерівномірного руху є такий, при якому швидкість тіла змінюється (збільшується чи зменшується) за будь-які рівні проміжки часу на однакову величину. Такий рух називають рівнозмінним.
Для того щоб охарактеризувати бистроту зміни швидкості тіла при рівнозмінному русі ввели поняття прискорення. Прискорення – це фізична величина, яка чисельно рівна зміні швидкості тіла за одиницю часу. Прискорення позначають літерою [а] і в СІ вимірюють в м/с2 . За означенням:
(1)
Як видно з формули (1) прискорення є векторною величиною і вектор прискорення колінеарний співнапрямлений з вектором зміни швидкості тіла за одиницю часу: 
.
Як вже зазначалось вище, при рівнозмінному русі швидкість тіла може збільшуватись чи зменшуватись на однакову величину. Тому виділяють два види рівнозмінного руху: рівноприскорений і рівносповільнений. Рівноприскорений – це такий рух, при якому швидкість тіла зростає за будь-які рівні проміжки часу на однакову величину, а рівносповільнений – це рух при якому швидкість тіла зменшується за будь-які рівні проміжки часу на однакову величину. Визначимо особливості рівноприскореного і рівносповільненого рухів.
При рівноприскореному русі 
, тому 
(при умові, що 
)..
При рівносповільненому русі 
, тому 
(при умові, що ).
Для того щоб дати відповідь на основне запитання кінематики (де буде тіло у конкретний момент часу) нам потрібно знати функціональну залежність між основними фізичними величинами, які характеризують рівнозмінний рух (координата, швидкість, прискорення, шлях, переміщення) і часом.
Оскільки швидкість тіла при рівнозмінному русі змінюється на однакову величину за будь-які рівні проміжки часу, то під час рівнозмінного руху прискорення тіла є величиною сталою (не залежить від часу). Отже, рівняння прискорення для рівнозмінного руху має вигляд 
(2).
З означення прискорення (1) можна виразити миттєву швидкість тіла 
і отримати залежність миттєвої швидкості від часу:
(3)
де - миттєва швидкість тіла в момент часу t;
- початкова швидкість тіла (в момент часу t0=0 );
- прискорення руху тіла.
Рівняння (3) можна переписати і в проекціях на осі координат, наприклад на вісь ОХ: 
, де 
- проекції відповідних векторів на вісь ОХ.
Рівняння шляху s для рівнозмінного руху в проекціях на деяку вісь, наприклад ОХ, матиме вигляд:
(4)
Врахувавши, що 
(де х – координата тіла в момент часу t, а х0 – координата тіла в момент часу t0=0) рівняння координати для рівнозмінного руху матиме вигляд:
(5)
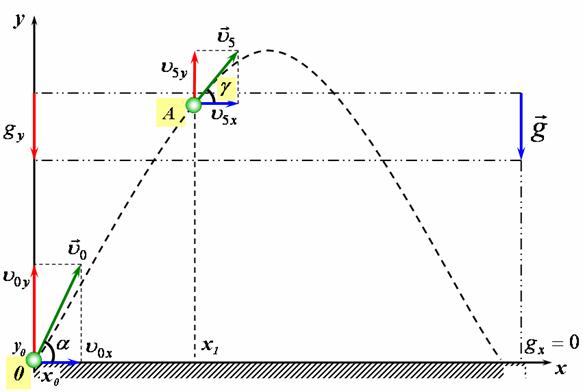
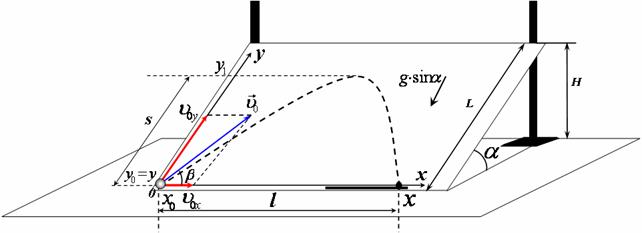
Знайдемо дальність польоту і максимальну висоту підняття тіла, кинутого під кутом 
до горизонту. Для цього зобразимо схему руху (рис 1). Оскільки рух тіла, кинутого під кутом до горизонту відбувається у вертикальній площині, то нам знадобляться дві взаємо перпендикулярні осі ОХ та OY для його описання.
Пов’яжемо систему відліку з землею. Вісь ОХ спрямуємо вздовж поверхні землі, а вісь OY вертикально вгору перпендикулярно до поверхні землі. Початок координат сумістимо з точкою початкового положення тіла, тоді з рис.2 Запишемо рівняння руху в проекціях на кожну вісь:
|
рис 1 |
та 
.
Оскільки під час польоту на кинуте тіло діє лише сила земного тяжіння, то тіло, кинуте під кутом до горизонту рухатиметься з прискоренням вільного падіння g. Спроектувавши вектори початкової швидкості і прискорення 
на осі ОХ та OY (рис 1), запишемо рівняння руху для даного випадку:
(6)
звідки 
(7)
Підставимо (7) в (6): 
. За формулами зведення 
, тоді
 - дальність польоту тіла. |
Щоб знайти максимальну висоту підняття, запишемо рівняння руху та рівняння швидкості в проекціях на вісь OY, але не для всього часу польоту, а для польоту з точки, ордината якої 
в точку з ординатою 
.
та 
Як видно з рис 2 в точці з ординатою проекція миттєвої швидкості тіла на вісь OY дорівнює нулю: 
. Спроектуємо вектори початкової швидкості і прискорення на вісь ОХ та OY (рис 2), прийнявши до уваги, що 
:
(8) 
звідки 
(9)
Порівнявши формули (9) та (7) можна зробити висновок, що час підйому тіла до найвищої точки траєкторії дорівнює половині часу всього руху тіла.
Підставивши (9) в (8) та виконавши математичні перетворення отримаємо:
 - максимальна висота підняття |
З отриманого співвідношення для дальності польоту слідує, що вона буде максимальною (для фіксованого значення 
) при максимальному значенні тригонометричної функції, тобто при 
, звідки 
.
Значення h буде найбільшим (для фіксованого значення ) при 
, звідки 
.
рис 2 |
Якщо площина, в якій відбувається рух тіла, кинутого під кутом не вертикальна, то слід спроектувати вектор прискорення не лише на осі ОХ та OY, а й на площину XOY, в якій відбувається рух 
. Для випадку, коли площина утворює з горизонтом кут (рис 2) рівняння (6) та (7) набудуть вигляду:
(10)
звідки 
(11)
Підставимо (11) в (10): 
звідки
 |
Аналогічно можна знайти максимальну висоту підняття кульки вздовж похилої площини s, доповнивши рівняння (8) та (9):
(13)
звідки 
(14)
Підставимо (14) в (13):
 |
Тоді висота підняття кульки над поверхнею парти: 
Контрольні запитання
1) Сформулюйте означення рівно змінного руху. Які види рівнозмінного руху Вам відомі та які їх особливості?
2) Сформулюйте означення прискорення рівнозмінного руху та запишіть формулу за якою визначається прискорення. Наведіть математичний запис законів рівнозмінного руху та назвіть величини, що входять до кожного з рівнянь.
3) Доведіть формулу для дальності польоту та максимальної висоти підняття тіла, кинутого під кутом до горизонту (зобразіть схему руху).
Розв’яжіть тренувальні задачі
1) Доведіть формулу для дальності польоту l, висоти підняття вздовж осі s та над горизонтальною поверхнею h тіла, кинутого під кутом 
до горизонту у полі сили тяжіння, якщо рух відбувається у площині, нахиленій під кутом до горизонту для таких значень кутів: 1) =300, =600; 2) =300, =450; 3) =450, =600. (зобразіть одну для всіх випадків схему руху).
2) Визначте максимальну висоту підняття тіла та його дальність польоту, якщо це тіло кинули під кутом 200 до горизонту з початковою швидкістю 20 м/с.
3) Визначте початкову швидкість тіла, кинутого під кутом 650 до горизонту, якщо дальність польоту тіла складає 80 м.
Хід роботи
І. Визначення початкової швидкості тіла, кинутого під кутом до горизонту, у полі сили
тяжіння.
1. Опрацюйте теоретичні відомості та інструкцію лабораторної роботи. Підготуйте у роботі таблицю даних 1 для запису результатів вимірювань та обчислень.
2. За допомогою штативу встановіть дерев’яну площину під кутом =450 до горизонту. Для цього виміряйте довжину фанери L. Висоту, на яку потрібно підняти її верхній край Н розрахуйте за формулою 
(рис 2)
3. Встановіть пусковий механізм під кутом =450 до нижнього краю дошки. Зробіть пробний постріл. У місці падіння кульки, на рівні з пусковим механізмом, на нижній край дошки прикріпіть смужку з пластиліну, щоб в результаті наступних пострілів падаюча кулька прилипала до нього. Запишіть значення кутів та до таблиці 1.
4. Зробіть запуск кульки та за допомогою мірної стрічки виміряйте її дальність польоту l (відстань від місця запуску до місця падіння кульки). Виконайте серію пострілів (не менше 5), щоразу вимірюючи дальність польоту. Знайдіть середню дальність польоту кульки lср. Отримані дані запишіть до таблиці 1.
5. Обчисліть початкову швидкість кульки за формулою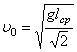 
та запишіть її значення до таблиці даних 1.
6. Знаючи початкову швидкість обчисліть максимальну висоту підняття кульки вздовж похилої площини s та над поверхнею парти h.
7. Обрахуйте та запишіть похибки вимірювань.
8. Повторіть дослід (пункти 2 – 7), розташовуючи пусковий механізм під такими кутами: 1) =300, =600; 2) =300, =450; 3) =450, =600.
9. Зробіть висновок, у якому опишіть свої здобутки, яких Ви набули, виконуючи дану роботу; головні причини похибок; основні, на Ваш погляд, недоліки та переваги даного дослідження; пропозиції щодо його покращення.
ІІ. Визначення виду траєкторії тіла, кинутого під кутом до горизонту у полі сили
тяжіння.
1. Опрацюйте теоретичні відомості та інструкцію лабораторної роботи. Підготуйте у роботі таблицю даних 2 для запису результатів вимірювань та обчислень.
2. За допомогою штативу встановіть дерев’яну площину під кутом =450 до горизонту. Для цього виміряйте довжину фанери L. Висоту, на яку потрібно підняти її верхній край Н розрахуйте за формулою . Встановіть пусковий механізм під кутом =450 до нижнього краю дошки.
3. На аркуші міліметрового паперу накресліть координатну сітку та прикріпіть до похилої площини так, щоб початок координат збігався точкою запуску кульки. Визначивши в попередньому досліді І початкову швидкість кульки, запишіть рівняння залежності координати кульки вздовж кожної з осей від часу х(t) та y(t) та рівняння траєкторії у(х).
4. Використовуючи дані рівняння теоретично розрахуйте координати та позначте на аркуші паперу відповідні положення кульки через кожні 0,05 с. Результати обчислень запишіть до складеної Вами таблиці даних 2. Через позначені точки проведіть плавну криву, яка і буде траєкторією руху кульки.
5. Після чого несильно змочіть кульку у воді та запустіть. На папері утвориться мокрий слід, який і буде реальною траєкторією кульки. Наведіть її олівцем. Підпишіть теоретично розраховану та експериментальну траєкторії на вашому рисунку. Продемонструйте отримані криві вчителю.
6. Зробіть висновок, у якому опишіть свої здобутки, яких Ви набули, виконуючи дану роботу; головні причини похибок; основні, на Ваш погляд, недоліки та переваги даного дослідження; пропозиції щодо його покращення.
Приклад таблиці:
Немає коментарів:
Дописати коментар